このブログにアクセスくださいましてありがとうございます。
この記事はグラフィックデザイナーで、姓名判断研究家のネコヒートが書いております。
今年も懲りずにチャレンジです。
プロ野球「2024年セ・リーグの順位」を姓名判断で占ってみました。
まずは、順位のおさらいから。
2023年の実際のセ・リーグはこんな順位でした。
| チーム | 差 | |
| 1 | 阪神 | — |
| 2 | 広島 | 11.5 |
| 3 | DeNA | 0.5 |
| 4 | 巨人 | 3.5 |
| 5 | ヤクルト | 13.5 |
| 6 | 中日 | 0.0 |
2023シーズンから監督に就任した岡田阪神が、ダントツで優勝。
逆に、2022年1位だったヤクルトは、中日と並んで「ほぼ最下位」でした。
予想外の躍進は、新井監督に代わった、広島カープ。選手とともに一喜一憂するシーンをよく見かけましたが、そういう「野球を一緒に楽しむ姿勢」が若い選手の多いチームにフィットしたせいもあるのかな。一方、優勝争いするかなと思っていた横浜DeNAは3位に後退しました。
球界の盟主・巨人も(悪い方の)予想外で、なんとBクラス。原さん、ちょっと年を取りすぎましたかね?強かった頃の采配とナンカ違うんですよね。そして、残念ながら、監督は、原さんから阿部慎之助監督に交代してしまいました。
さて、占った結果はと言いますと…
| チーム | |
| 1 | DeNA |
| 2 | 広島 |
| 3 | 巨人 |
| 4 | ヤクルト |
| 5 | 阪神 |
| 6 | 中日 |
うーん、阪神の順位が思いっきり外れてますね。
しかし、阪神を1位に持っていくと、かなり最終的な順位に近くなるのです(言い訳です)。
| 2023結果 | ネコヒート | |
| 1 | 阪神 | 阪神 |
| 2 | 広島 | DeNA |
| 3 | DeNA | 広島 |
| 4 | 巨人 | 巨人 |
| 5 | ヤクルト | ヤクルト |
| 6 | 中日 | 中日 |
どうでしょう?
だいぶ近くなったような気がしませんか?
DeNAと広島が違うくらいなんですよ。
つまり、(手前味噌ですが)けっこう良い線を行っていたわけで、今年はさらに予想セットを、下記のように変えてみることにしました。
- 監督の名前
- ヘッドコーチの名前
- エース級投手の名前
- 主軸のバッターの名前
「戦いは現場で起きている」をモットーとすることは、今回も同じ。
現場主義を継続しながらも、実際に闘う、「投打の男たちの名前」を追加してみました。
これならいけるでしょう。
採点方法は、ネコヒート姓名判断で用いる「姓名判断ポイント」制。
簡単に言ってしまうと、ひとりひとりの名前全体の良し悪しを問う、ということになります。
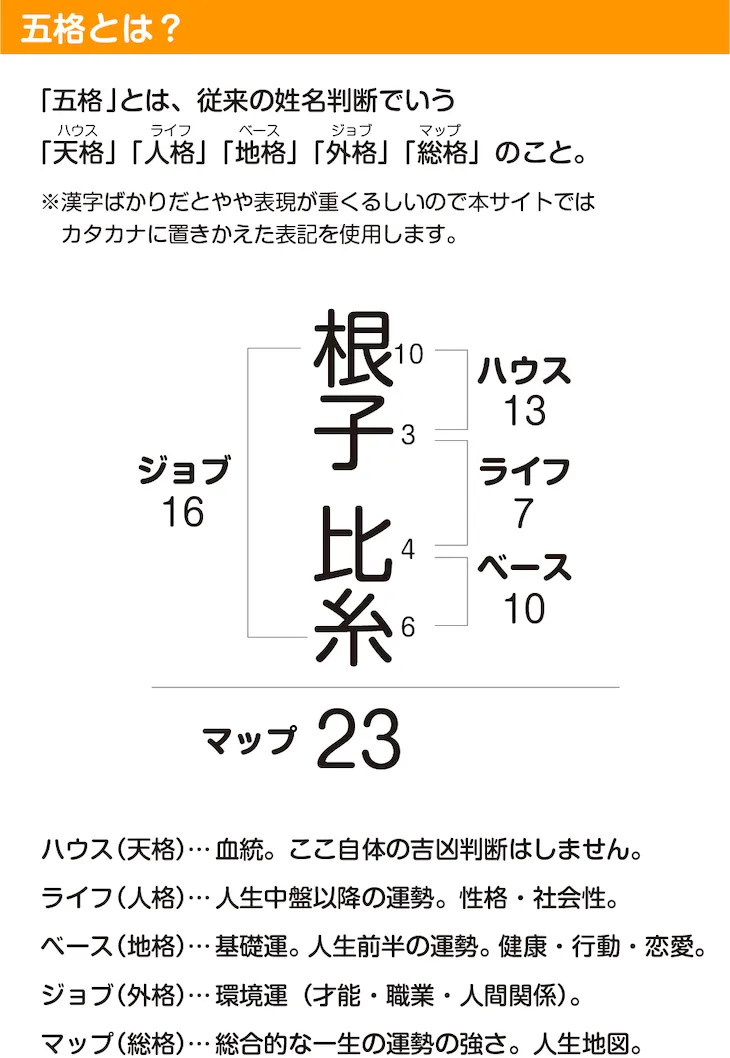
「姓名判断ポイント」の内訳は次の2つ。
- 画数のポイント(五格の吉凶)
- 三才配置のポイント(天人地の相性)
手順としては各チーム4名の、ひとりひとりの姓名判断ポイントを算出し、4人分のポイントを単純に合計して競ってみようというルールです。
(詳しいルールは、「付録:ルール・算出方法」をご覧ください。)
監督pt +ヘッドpt + 野手pt + 投手pt=合計pt
さて、今年も、プロ野球の開幕を前にひと足早い「名前勝負」を行ってみましょう。
姓名判断は当たるのでしょうか?
姓名判断の哲学が教える順位はどのようになったのでしょうか?
さあ、セ・リーグのランキング集計が終わりました。
かなり予想外の結果が出たようですよ。
今回は、第5位から第2位を発表します。
さっそく見てみましょう、
ドーッゾ!!
5位
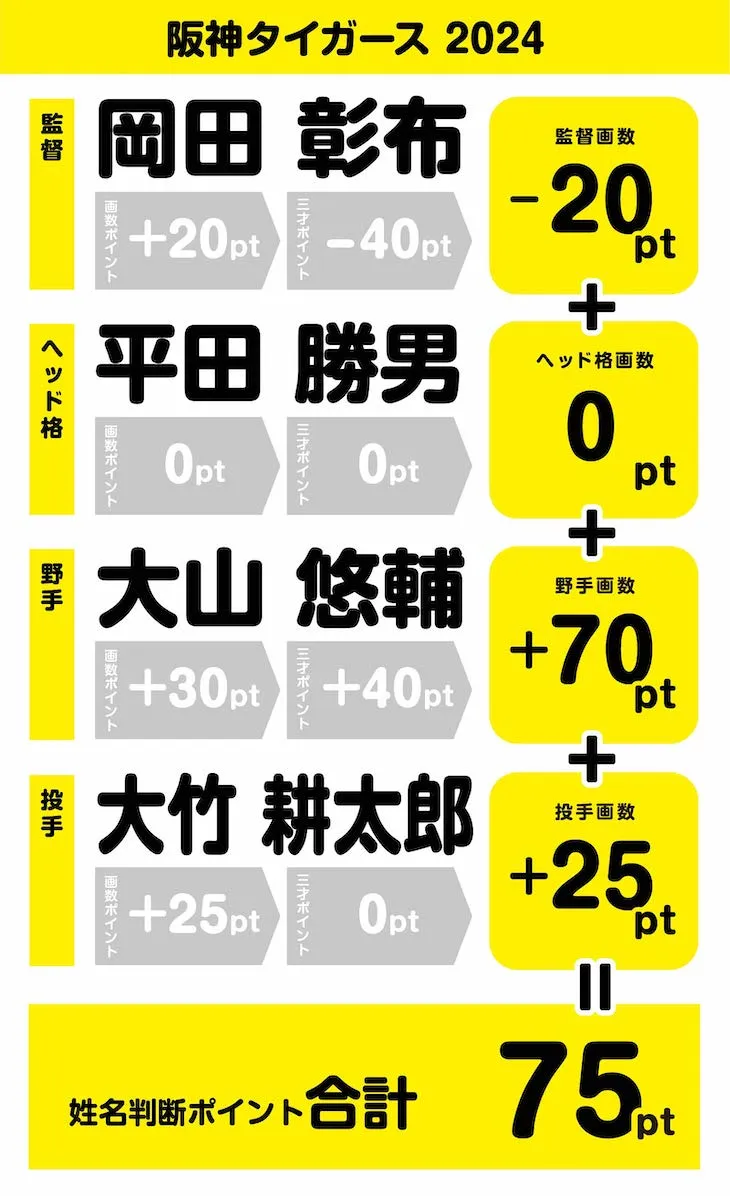
第5位は、なんと、2023年優勝チーム、阪神タイガースでした。
合計ポイントは75ポイント。
姓名判断チャートを掲載しましょう。
今年もタイガースが下位に沈みましたねぇ。姓名判断と相性が悪いのかな?
投打のメンバーは一新されましたね。
野手は、チームを支える四番打者・大山悠輔選手を。投手は昨年ソフトバンク・ホークスから移籍してきて予想外の大活躍を見せた大竹耕太郎投手を選出しました。
2人で95ポイントを叩き出しましたが、昨年同様、岡田監督と平田ヘッドが足を引っ張りましたね。
2人合わせて「-20pt」では、上位進出は望めません。
しかし、2023年シーズンの岡田采配はさすがの安定感でした。
「(采配としては)あまりやることなかった」と言っていたのは本音だと思います。
なにせセ・リーグは、若い(未熟な)監督ばかり。
熟練の渋い采配と渡り合える監督は残念ながら今はいません(強いてあげれば高津監督くらい)。そう言う意味では、2024シーズンも相変わらず楽勝の流れになってもまったく不思議ではないのですが、果たして…。
いずれにしましても、2024年セ・リーグの第5位は、阪神タイガースであると予想します。
続いて、第4位の発表です。
4位
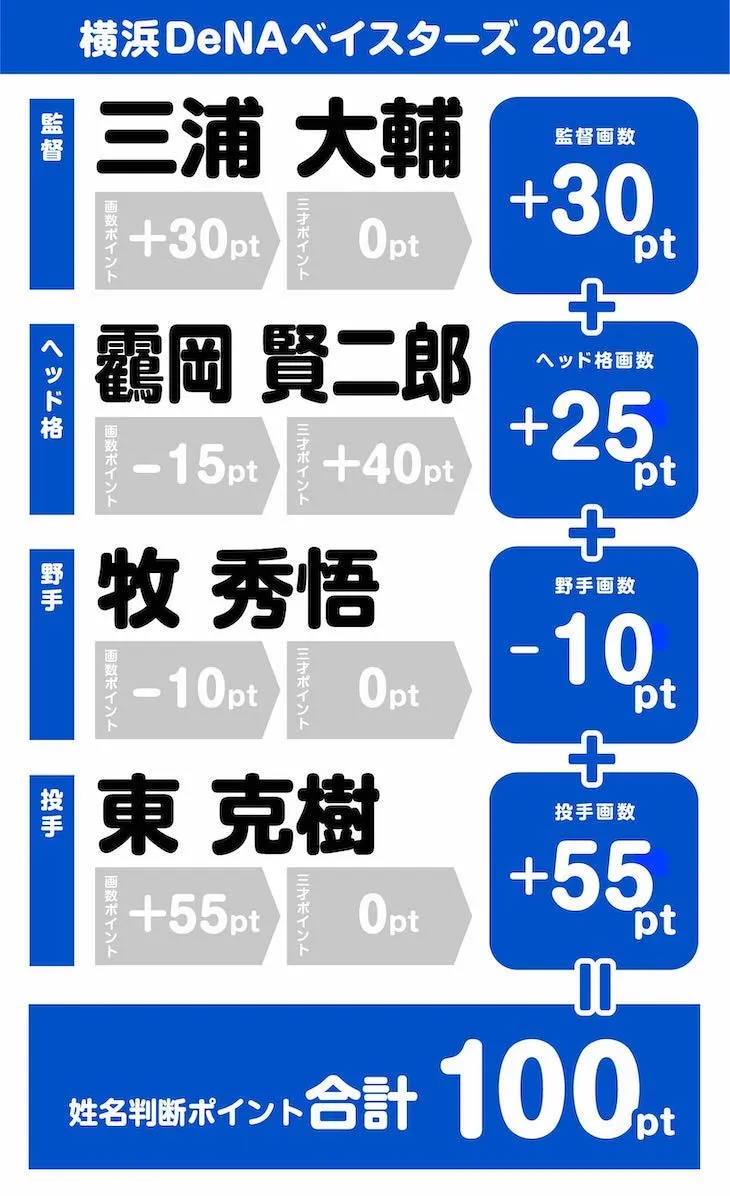
第4位は、横浜DeNAベイスターズでした。
合計ポイントは100ポイント。
姓名判断チャートを掲載しましょう。
昨年3位のベイスターズが4位に転落…。
しかし、2023年度、優勝出来なかったのは痛かったですねぇ。
2021年6位→2022年2位だったのだから、是が非でも優勝を狙うべきだったし、「持っている監督」なら優勝していたはずです。
予想セットの方は、監督以外は一新されました。
とくに目を引くのは「靏岡賢二郎」という名前でしょう。
これまでデータアナリストとして影ながらチームを支えていた人物ですが、今年から「ヘッド格」に昇格しました。
「わざわざデータアナリストをヘッド格に置く必要があるのかなぁ」と言う思いと、「さすがゲーム会社が親会社のチームだな、型にハマらないところは素晴らしい」という2つの気持ちが交錯する不思議な人事でした。
さて、これが吉と出るのか?凶と出るのか?
その他、今永投手、バウアー投手、ソト選手など相当な戦力ダウンをしていることからも、今年は相当苦戦しそうですね。
よって、セ・リーグ第4位は、DeNAベイスターズであると予想します。
続いて、ここからAクラス、第3位の発表です。
3位
第3位になったのは、2023年2位だった、広島カープでした。
合計ポイントは115ポイント。
姓名判断チャートを掲載しましょう。

2023年シーズンは、新井監督と藤井ヘッドという「良い名前コンビ」がハマって、なんと2位に大躍進しました。
2024年も、2位かそれ以上を狙うかと思いきや、意外と選手2名の名前が振るいませんでしたね。とくに板倉選手が足を引っ張りました。
野手には、板倉選手を選出しましたが、実は板倉選手はキャッチャーです。そんなに派手な活躍もしていません。
- 試合:120
- 打率:.266
- 本塁打:12
- 打点:44
キャッチャーとしては打てる捕手の部類に入るのでしょうが、かと言って中心打者というには物足りないわけです。
だからと言って、秋山翔吾選手も期待ハズレだったし、末包選手も未知数だし、小園選手は次世代の選手でしょうし、「この人」という野手が見当たらないのは、かなり苦しいシーズンになることを象徴してそうですよね。あと、西川龍馬選手のオリックスへの移籍も痛かったですねぇ。
というわけで、打つ方でかなり苦労しそうな、広島カープが第3位になると予想します。
第2位の発表です。
2位
第2位になったのは、2023年6位だった、中日ドラゴンズ。
驚きですねぇ。大躍進。合計ポイントは125ポイントでした。
姓名判断チャートを掲載しましょう。
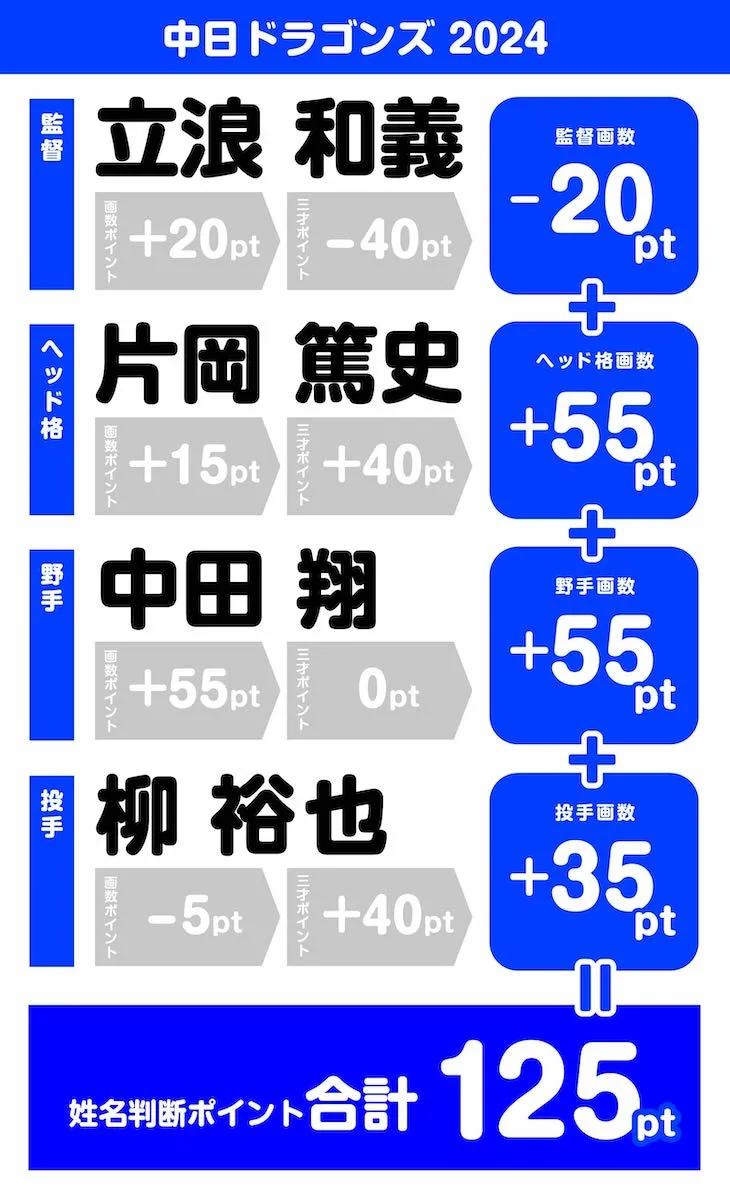
立浪監督は相変わらずのマイナスポイントでしたが、今シーズンからヘッド格に就いた、PL学園時代から仲良しの片岡篤史ヘッドと、今シーズン巨人から移籍してきた中田翔選手が堅実にポイントを稼ぎましたね。
そこに、もともと35ポイントネームの柳投手が加わり、信じられない大躍進となりそうな予感。
中日ファンとしてはうれしい順位ですが、そんな甘い話ありますかね?
問題は山積みだったはずなのです。
1点を取る野球がやたら下手くそなチームだったこと。
おもに立浪監督の責任ですが、今シーズン、その辺は解消できるのでしょうか?急に采配が上手になるなんてことがあるのでしょうかね(うーん、という感じ)?
コーチを差し置いて「教え魔」となり、意に染まない選手を干したり外に出したり、そういう昭和チックな「パワハラ野球」は改善できるのでしょうか?
そのあたりが変わらない限り、いや立浪監督自身が大きく変わらない限り、2位は難しそうですけどね…。
いずれにしましても、立浪監督が「見事に改心する」という前提で、第2位になるのは中日ドラゴンズであると予想します。
まとめ
さて、今回はここまでです。
順位をまとめまてみました。
| チーム | |
| 1 | ??? |
| 2 | 中日 |
| 3 | 広島 |
| 4 | DeNA |
| 5 | 阪神 |
| 6 | ??? |
残りの2チームは、「読売ジャイアンツ」と「ヤクルトスワローズ」です。
阿部監督率いる盟主が、復活のシーズンになるのでしょうか?
それとも、2度優勝の高津スワローズが、最下位から「V字大復活」を果たすのでしょうか?
2024年シーズン、優勝するのはどちらか?
次回、第6位と第1位を同時発表しますのでお楽しみに!
〈続く〉
付録:ルール・算出方法
今回の企画、2024年度のセ・リーグ優勝予想するにあたっては、マップ(総格)のみならず画数全体の吉凶をポイント化し競っています。
ネコヒート姓名判断内では「姓名判断ポイント」と呼んでいるものになります。
姓名判断ポイントは以下の二つで成り立っています。
- 画数ポイント
- 三才配置ポイント
画数ポイントは、五格の画数をそれぞれ導き出しポイント化したもの。
三才配置ポイントは、天格と人格、人格と地格の相性をポイント化したものです。
名前の画数の求め方、画数のポイント化に関しましては以下の記事で詳しくご紹介しています。